F n võrdub g-ga. Rekursioon ja rekursiivsed algoritmid. Puu kujutamine arvutimälus
Rekursioon on olukord, kus alamprogramm helistab ise. Esmakordselt sellise algoritmilise konstrueerimisega kokku puutudes tekib enamikul inimestel teatud raskusi, kuid väike harjutamine ja rekursioon muutub teie programmeerimise arsenalis arusaadavaks ja väga kasulikuks tööriistaks.
1. Rekursiooni olemus
Protseduur või funktsioon võib sisaldada kutset muudele protseduuridele või funktsioonidele. Protseduuri kaasamine võib põhjustada iseennast. Siin pole paradoksi - arvuti täidab programmis ilmnenud käske ainult järjestikku ja kui ta kohtub protseduurikõnega, hakkab ta seda protseduuri lihtsalt täitma. Pole tähtis, milline protseduur andis käsu seda teha.
Näide rekursiivsest protseduurist:
Protseduur Rec (a: täisarv); algab, kui a\u003e
Mõelge, mis juhtub, kui põhiprogrammis helistatakse näiteks vormis Rec (3). Allpool on vooskeem, mis näitab avalduste jada.
Joon. 1. Rekursiivse protseduuri plokkskeem.
Rec-protseduuri kutsutakse parameetriga a \u003d 3. See sisaldab üleskutset Rec-protseduurile parameetriga a \u003d 2. Eelmine kõne pole veel lõpule jõudnud, nii et võite ette kujutada, et luuakse mõni teine \u200b\u200bprotseduur ega lõpeta oma esimest tööd enne selle lõppu. Kõneprotsess lõpeb, kui parameeter a \u003d 0. Sel hetkel teostatakse korraga 4 protseduuri esinemisjuhtu. Kutsutakse korraga teostatud protseduuride arvu rekursiooni sügavus.
Neljas protseduur (Rec (0)) prindib numbri 0 ja lõpetab oma töö. Pärast seda naaseb juhtseadis seda kutsunud protseduuri juurde (Rec (1)) ja trükitakse number 1. Ja nii edasi, kuni kõik protseduurid on lõpule viidud. Esialgse kõne tulemuseks on nelja numbri printimine: 0, 1, 2, 3.
Veel üks visuaalne pilt toimuvast on esitatud joonisel fig. 2

Joon. 2. Rec-protseduuri läbiviimine parameetriga 3 hõlmab Rec-protseduuri täitmist parameetriga 2 ja numbri 3 printimist. Omakorda Rec-protseduuri täitmine parameetriga 2 koosneb Rec-protseduuri teostamisest parameetriga 1 ja numbri 2 printimisest jne.
Iseseisva treeninguna mõelge, mis juhtub, kui helistate Rec (4). Mõelge ka sellele, mis juhtub, kui helistate allpool kirjeldatud protseduurile Rec2 (4), kus operaatorid on ümber pööratud.
Protseduur Rec2 (a: täisarv); algavad kirjutised (a); kui a\u003e 0, siis Rec2 (a-1); lõpp;
Pange tähele, et ülaltoodud näidetes on rekursiivne kõne tingimuslause sees. See on rekursiooni lõpliku lõppemise eeltingimus. Pange tähele ka seda, et protseduur ise kutsub teistsuguse parameetriga, mitte samaga, millega seda kutsuti. Kui protseduur ei kasuta globaalseid muutujaid, on vajalik ka, et rekursioon ei jätkuks määramata aja jooksul.
Võimalik on pisut keerulisem skeem: funktsioon A kutsub funktsiooni B ja see omakorda kutsub A. Seda kutsutakse keeruline rekursioon. Sel juhul selgub, et esimeses kirjeldatud protseduur peaks põhjustama veel kirjeldamata jätmist. Selle võimaldamiseks on vaja kasutada.
Protseduur A (n: täisarv); (Esimese protseduuri eelkirjeldus (pealkiri)) protseduur B (n: täisarv); (Teise protseduuri eelkirjeldus) protseduur A (n: täisarv); (Protseduuri A täielik kirjeldus) alustada kirjutist (n); B (n-1); lõpp; protseduur B (n: täisarv); (Protseduuri B täielik kirjeldus) algab writeln (n); kui n
Protseduuri B täpsem kirjeldus võimaldab seda kutsuda protseduurist A. Selles näites protseduuri A täpsem kirjeldus pole esteetilistel põhjustel vajalik ja lisatud.
Kui tavalist rekursiooni saab võrrelda meieoborosega (joonis 3), saab keeruka rekursiooni pildi saada kuulsast lasteluuletusest, kus “Hundid ehmusid, sõid üksteist”. Kujutage ette, kuidas kaks hunti söövad üksteist, ja saate aru keerulisest rekursioonist.

Joon. 3. Ouroboros - madu, kes sööb saba. Joonis Theodor Pelekanose (1478) alkeemilisest traktaadist “Synosius”.

Joon. 4. Kompleksne rekursioon.
3. Silmuse simuleerimine rekursiooni abil
Kui protseduur kutsub ennast esile, siis sisuliselt viib see selles sisalduvate juhiste korduva täitmiseni, mis sarnaneb tsükli toimimisega. Mõni programmeerimiskeel ei sisalda üldse tsüklilisi konstruktsioone, jättes programmeerijatele korduste korraldamise rekursiooni abil (näiteks Prolog, kus rekursioon on peamine programmeerimistehnika).
Näiteks simuleerige a-loo töö. Selleks vajame muutuja sammu loendurit, mida saab rakendada näiteks protseduuriparameetrina.
Näide 1
Protseduuri silmus (i, n: täisarv); (Esimene parameeter on sammude loendur, teine \u200b\u200bparameeter on sammude koguarv) alustage kirjutist ("Tere N", i); // Siin on kõik juhised, mida korratakse, kui i Tüübi LoopImitation (1, 10) kõne tulemus on käskude kümnekordne täitmine, loenduri muutusega 1 kuni 10. Sel juhul prinditakse see: Tere, N 1 Üldiselt ei ole keeruline mõista, kas protseduuri parameetrid on loenduri väärtuste muutuse piirid. Nagu järgmises näites, saate vahetada rekursiivset kõnet ja juhiseid korrata. Näide 2
Protseduuri silmusImiteerimine2 (i, n: täisarv); alustada, kui i Sel juhul tuleb enne juhiste täitmist alustada protseduuri rekursiivset kutset. Menetluse uus eksemplar kutsub esiteks ka teise eksemplari ja nii edasi, kuni jõuame loenduri maksimaalse väärtuseni. Alles pärast seda täidab viimane kutsutud protseduuridest oma juhised, siis täidab ta oma eelviimaseid juhiseid jne. LoopImitation2 (1, 10) helistamise tulemus prindib tervitused vastupidises järjekorras: Tere, N 10 Kui kujutate ette rekursiivselt nimetatavate protseduuride ahelat, siis näites 1 läbime selle varem kutsutud protseduuridest hilisemateni. Näites 2 on hilisemast varasem vastupidine. Lõpuks saab kahe juhisteploki vahele panna rekursiivse kõne. Näiteks: Protseduuri silmuslimiit3 (i, n: täisarv); algavad kirjutised ("Tere N", i); (Esimene juhiste blokk võib paikneda siin), kui i Esiteks täidetakse järjestikku esimese ploki juhised, seejärel vastupidises järjekorras teise ploki juhised. LoopImitation3 (1, 10) helistades saame: Tere, N 1 Sama tegemine ilma rekursioonita võtab kaks tsüklit korraga. Võib kasutada asjaolu, et sama protseduuri osade täitmine on ajaliselt eraldatud. Näiteks: Näide 3: Numbri teisendamine binaarsüsteemiks.
Binaarse numbri numbrite saamine, nagu teate, toimub jagamisel ülejäänud osaga numbrisüsteemi 2 aluses. Kui arv on olemas, siis on selle kahendkujul selle viimane number Arvestades täisarvu jagamist kahega: saame arvu, millel on sama binaarne esitus, kuid ilma viimase numbrita. Seega piisab kahe ülaltoodud toimingu korramisest, kuni järgmise jagamisvälja täisarv saab võrdseks nulliga. Ilma rekursioonita näeb see välja järgmine: Kui x\u003e 0, alustage c: \u003d x mod 2; x: \u003d x div2; kirjuta (c); lõpp; Probleem on selles, et binaarse esituse numbrid arvutatakse vastupidises järjekorras (esimene viimane). Numbri tavapärasel kujul printimiseks peate meeles pidama kõik massiivi elementide numbrid ja kuvama selle eraldi tsüklis. Rekursiooni kasutades on väljundit õiges järjekorras lihtne saada ilma massiivi ja teise ahelata. Nimelt: Protseduur Binaarneesindamine (x: täisarv); var c, x: täisarv; alustada (Esimene plokk. See täidetakse protseduurikõne järjekorras) c: \u003d x mod 2; x: \u003d x div2; (Rekursiivne kõne), kui x\u003e 0, siis BinaryRepresentation (x); (Teine plokk. See täidetakse vastupidises järjekorras) write (c); lõpp; Üldiselt pole me mingit kasu saanud. Binaarse esituse numbrid salvestatakse kohalikesse muutujatesse, mis on rekursiivse protseduuri igal tööastmel erinevad. See tähendab, et mälu polnud võimalik salvestada. Vastupidi, me kulutame lisamälu paljude kohalike muutujate x salvestamiseks. Sellegipoolest tundub selline lahendus minu jaoks ilus. Öeldakse, et vektorite jada antakse kordussuhtega, kui algvektor ja järgneva vektori funktsionaalne sõltuvus eelmisest Kordussuhete abil arvutatud koguse lihtne näide on faktoriaal Järgmise teguri saab eelmisest arvutada järgmiselt: Märgistust tutvustades saame suhte: Valemile (1) vastavaid vektoreid saab tõlgendada muutuvate väärtuste komplektidena. Siis koosneb jada vajaliku elemendi arvutamine nende väärtuste korduvast värskendamisest. Eelkõige faktoriaalide jaoks: X: \u003d 1; i jaoks: \u003d 2 kuni n do x: \u003d x * i; kirjutis (x); Iga selline värskendus (x: \u003d x * i) kutsutakse iteratsioon, ja iteratsioonide kordamise protsess on iteratsioon. Märgime siiski, et seos (1) on jada puhtalt rekursiivne määratlus ja n-nda elemendi arvutamine on tegelikult funktsiooni f mitu korduvat võtmist: Faktorite jaoks võite kirjutada: Funktsionaalne faktoriaal (n: täisarv): täisarv; alustage, kui n\u003e 1, siis Faktoriaal: \u003d n * Faktoriaal (n-1) muidu Faktoriaal: \u003d 1; lõpp; Tuleks mõista, et funktsioonide kutsumine toob endaga kaasa teatavaid lisakulutusi, nii et esimene võimalus faktoriaal arvutamiseks on mõnevõrra kiirem. Üldiselt toimivad iteratiivsed lahendused kiiremini kui rekursiivsed. Enne kui liikuda olukordadesse, kus rekursioon on kasulik, pöörake tähelepanu veel ühele näitele, kus seda ei tohiks kasutada. Mõelge kordumissuhete erijuhule, kui järgmine väärtus jadas ei sõltu mitte ühest, vaid kohe mitmest eelmisest väärtusest. Näitena võib tuua tuntud Fibonacci jada, milles iga järgmine element on kahe eelneva summa: Frontaalse lähenemise korral saate kirjutada: Funktsiooni kiud (n: täisarv): täisarv; alusta, kui n\u003e 1, siis Fib: \u003d Fib (n-1) + Fib (n-2) muidu Fib: \u003d 1; lõpp; Iga Fib-kõne loob ise kaks koopiat, iga koopia loob veel kaks koopiat jne. Operatsioonide arv kasvab koos arvuga n plahvatuslikult, kuigi iteratiivne lahendus on piisavalt lineaarne n operatsioonide arv. Tegelikult see näide meid ei õpeta MILLAL rekursiooni ei tohiks kasutada, kuid Kuidas seda ei tohiks kasutada. Lõpuks, kui on olemas kiire iteratiivne (silmuspõhine) lahendus, saab sama ahela rakendada ka rekursiivse protseduuri või funktsiooni abil. Näiteks: // x1, x2 - algtingimused (1, 1) // n - vajaliku Fibonacci arvu funktsiooni number Fib (x1, x2, n: täisarv): täisarv; var x3: täisarv; alusta, kui n\u003e 1, siis alusta x3: \u003d x2 + x1; x1: \u003d x2; x2: \u003d x3; Fib: \u003d Fib (x1, x2, n-1); lõpp muidu Fib: \u003d x2; lõpp; Siiski eelistatakse iteratiivseid lahendusi. Küsimus on selles, millal tuleks siis rekursiooni kasutada? Kõik rekursiivsed protseduurid ja funktsioonid, mis sisaldavad ainult ühte rekursiivset kõnet, on hõlpsasti asendatavad iteratiivsete tsüklitega. Et saada midagi, millel pole lihtsat mitterekursiivset analoogi, peaksite pöörduma protseduuride ja funktsioonide poole, mis kutsuvad ennast kaks või enam korda. Sel juhul ei moodusta kutsutud protseduuride komplekt enam ahelat, nagu joonisel fig. 1 ja kogu puu. Kui arvutusprotsess tuleks sel viisil korraldada, on laias laastus probleeme. Just nende jaoks on rekursioon selle lahendamiseks kõige lihtsam ja loomulikum viis. Korduvalt end nimetavate rekursiivsete funktsioonide teoreetiline alus on diskreetse matemaatika osa, mis uurib puid. Definitsioon:
me kutsume piiratud komplekti Tkoosneb ühest või enamast sõlmest, nii et: See määratlus on rekursiivne. Lühidalt öeldes: puu on kogum, mis koosneb juurest ja selle külge kinnitatud alampuudest, mis on ka puud. Puu määratletakse iseenda kaudu. See määratlus on siiski tähenduslik, kuna rekursioon on piiratud. Iga alampuu sisaldab vähem sõlmi kui selle puu. Lõpuks jõuame alamtreasidesse, mis sisaldavad ainult ühte sõlme, ja on juba selge, mis see on. Joon. 3. Puu. Joon. Joonis 3 kujutab seitsme sõlmega puud. Ehkki tavalised puud kasvavad alt üles, on nende joonistamine vastupidine. Diagrammi käsitsi joonistades on see meetod ilmselgelt mugavam. Selle ebajärjekindluse tõttu tekib mõnikord segadust, kui nad ütlevad, et üks sõlme asub teisest kõrgemal või all. Sel põhjusel on mugavam kasutada sugupuude kirjeldamiseks kasutatavat terminoloogiat, kutsudes juurte esivanematele lähemal asuvaid sõlmi ja kaugemaid järeltulijaid. Graafiliselt saab puud esitada mitmel muul viisil. Mõned neist on esitatud joonisel fig. 4. Puu on definitsiooni järgi pesastatud komplektide süsteem, kus need komplektid kas ei ristu või on täielikult üksteisega seotud. Selliseid komplekte saab kujutada piirkondadena tasapinnal (joonis 4a). Joon. 4b, ei paikne pesastatud komplektid tasapinnal, vaid on pikitud ühe joonega. Joon. 4b võib pidada ka mõne pesastatud sulgudes sisalduva algebralise valemi diagrammiks. Joon. 4c pakub veel ühte populaarset viisi puustruktuuri loendina kuvamiseks. Joon. 4. Muud viisid puustruktuuride esindamiseks: a) pesakomplektid; b) pesad; c) ülesandeloend. Suunatud loendil on koodi vormindamise osas ilmseid sarnasusi. Struktuurilise programmeerimise paradigma raames kirjutatud programmi saab tõepoolest kujutada puuna, mis koosneb pesastatud konstruktsioonidest. Samuti saate joonistada analoogia ülesannete loendi ja sisukorra ilmumise vahel raamatutes, kus jaotised sisaldavad alajaotusi, need omakorda alajaotused jne. Selliste lõikude (jaotis 1, alajaod 1.1 ja 1.2, alajaotis 1.1.2 jne) tavapärast nummerdamise viisi nimetatakse Dewey kümnendsüsteemiks. Nagu joonisel fig. 3 ja 4, annab see süsteem: 1. A; 1,1 B; 1,2 ° C; 1.2.1 D; 1,2,2 E; 1.2.3 F; 1.2.3.1 G; Kõigis puustruktuuridega seotud algoritmides esineb alati sama mõte, nimelt idee mööduv või puu liikumine. See on puu sõlmede külastamise viis, kus iga sõlm läbib täpselt ühe korra. Selle tulemuseks on puusõlmede lineaarne paigutus. Eelkõige on kolm viisi: saate läbida sõlmed nii edasi, tagasi kui ka lõpu järjekorras. Läbilõike algoritm otseses järjekorras: See algoritm on rekursiivne, kuna puu liikumine sisaldab läbitavaid alamtreesid ja need omakorda läbivad sama algoritmi. Eriti joonisel fig. 3 ja 4, annab otsene läbimine sõlmede jada: A, B, C, D, E, F, G. Saadud jada vastab järjestikusele sõlmede loendile vasakult paremale, kui puu esindatakse pesastatud sulgudes ja Dewey kümnendsüsteemis, ning ülalt alla, kui see on esitatud omistamisloendi kujul. Selle algoritmi programmeerimiskeeles juurutamisel vastab juurini jõudmine mõne toimingu protseduuri või funktsiooni täitmisele ja alampride suunamisele iseendale rekursiivsete kõnede saamiseks. Täpsemalt, binaarse puu puhul (kui igast sõlmest ei tule rohkem kui kaks alampuud) näeb vastav protseduur välja järgmine: // Preorder Traversal - ingliskeelne nimi otseturunduse protseduuriks PreorderTraversal ((Argumendid)); alusta // juure DoSomething ülekandmine ((Argumendid)); // Mööda vasakpoolne alampuu, kui (On olemas vasakpoolne alampuu), siis PreorderTransversal ((Argumendid 2)); // Minge parem alampuu, kui (On olemas parem alampuu), siis PreorderTransversal ((Argumendid 3)); lõpp; See tähendab, et algul sooritab protseduur kõik toimingud ja alles siis esinevad kõik rekursiivsed kõned. Traversialgoritm vastupidises järjekorras: See tähendab, et kõik alamristad suunatakse vasakult paremale ja tagasipöördumine juure asub nende lõikude vahel. Puu jaoks joon. 3 ja 4 annab see sõlmede jada: B, A, D, C, E, G, F. Vastava rekursiivse protseduuri korral asuvad toimingud rekursiivsete kõnede vahel. Eriti kahekomponentsete puude puhul: // Inorder Traversal - ingliskeelne nimi vastupidises järjekorras InorderTraversal ((Arguments)); alusta // Liigu vasakpoolne alampuu, kui (On vasakpoolne alampuu), siis InorderTraversal ((Argumendid 2)); // Juur DoSomething ((Argumendid)) edastamine; // Minge parem alampuu, kui (On olemas parem alampuu), siis InorderTraversal ((Argumendid 3)); lõpp; Läbiviimise algoritm lõppjärjestuses: Puu jaoks joon. 3 ja 4 annab see sõlmede jada: B, D, E, G, F, C, A. Vastavas rekursiivses protseduuris asuvad toimingud pärast rekursiivseid kõnesid. Eriti kahekomponentsete puude puhul: // Postorder Traversal - ingliskeelne nimi lõpptellimuse protseduurile PostorderTraversal ((Argumendid)); alusta // Liigu vasakpoolne alampuu, kui (On vasakpoolne alampuu), siis PostorderTraversal ((Argumendid 2)); // Minge parem alampuu, kui (On olemas parem alampuu), siis PostorderTraversal ((Argumendid 3)); // Juur DoSomething ((Argumendid)) edastamine; lõpp; Kui mingi teave asub puu sõlmedes, saate selle salvestamiseks kasutada vastavat dünaamilist andmestruktuuri. Pascali puhul kasutatakse seda muutuja tüüpi kirjet, mis sisaldab osi sama tüüpi alamainetele. Näiteks saab binaarset puud, kus iga sõlm sisaldab täisarvu, salvestada PTree tüüpi muutuja abil, mida kirjeldatakse allpool: Tüüp PTree \u003d ^ TTree; TTree \u003d kirje inf: täisarv; LeftSubTree, RightSubTree: PTree; lõpp; Iga sõlme tüüp on PTree. See on osuti, see tähendab, et iga sõlm tuleb luua, kutsudes selle jaoks uue protseduuri. Kui sõlmeks on lõppsõlm, omistatakse selle väljadele LeftSubTree ja RightSubTree väärtus null. Muul juhul luuakse uue protseduuri abil ka sõlmed LeftSubTree ja RightSubTree. Skemaatiliselt on üks selline rekord näidatud joonisel fig. 5 Joon. 5. TTree tüüpi kirje skemaatiline illustratsioon. Kirjel on kolm välja: Inf - teatud arv, LeftSubTree ja RightSubTree - viited sama tüüpi TTree kirjetele. Sellistest kirjetest koosneva puu näide on toodud joonisel 6. Joon. 6. TTree-kirjetest koosnev puu. Igas kirjes on number ja kaks osutit, mis võivad sisaldada kumbagi nullvõi muude sama tüüpi kirjete aadressid. Kui te pole varem töötanud struktuuridega, mis koosnevad kirjetest, mis sisaldavad linke sama tüüpi kirjetele, soovitame teil lugeda materjali selle kohta. Mõelge joonisel fig. 1 näidatud puu joonistamise algoritmile. 6. Kui arvestame iga rida sõlmena, siis vastab see pilt täielikult puu eelmises jaotises esitatud määratlusele. Joon. 6. Puu. Rekursiivne protseduur peaks ilmselgelt tõmbama ühe joone (pagasiruumi enne esimest haru) ja kutsuma ennast siis kaks alamjooksu joonistama. Alampuud erinevad neid sisaldavast puust lähtepunkti koordinaatide, pöördenurga, pagasiruumi pikkuse ja neis asuvate harude arvu järgi (üks vähem). Kõik need erinevused tuleks teha rekursiivse protseduuri parameetrite järgi. Allpool on esitatud sellise protseduuri näide, mis on kirjutatud Delfis: Protseduuripuu (lõuend: TCanvas; // lõuend, millele tõmmatakse x, y: laiendatud puu; // Juure nurga koordinaadid: pikendatud; // Puu kasvamise nurk TrunkLength: pikendatud; // Pagasiruumi pikkus n: täisarv / / Filiaalide arv (kui palju veel // rekursiivseid kõnesid on veel ees); var x2, y2: laiendatud; // pagasiruumi ots (hargnemispunkt) algab x2: \u003d x + TrunkLength * cos (Nurk); y2: \u003d y - TrunkLength * sin (Nurk); Canvas.MoveTo (ümmargune (x), ümar (y)); Canvas.LineTo (ümmargune (x2), ümmargune (y2)); kui n\u003e 1, alustage puu (lõuend, x2, y2, Nurk + Pi / 4, 0,55 * TrunkLength, n-1); Puu (lõuend, x2, y2, Angle-Pi / 4, 0,55 * TrunkLength, n-1); lõpp; lõpp; Joon. 6, kutsuti seda protseduuri järgmiste parameetritega: Puu (Image1.Canvas, 175, 325, Pi / 2, 120, 15); Pange tähele, et joonistamine toimub enne rekursiivseid kõnesid, see tähendab, et puu joonistatakse otseses järjekorras. Legendi kohaselt on Benarase linna suures templis, maailma keset tähistava katedraali all pronksketas, millele on kinnitatud 3 teemantvarrast, ühe küünarnuki kõrgus ja mesilase paksus. Kunagi ammu, üsna aegade alguses, olid selle kloostri mungad jumala Brahma ees süüdi. Vihaselt püstitas Brahma kolm kõrget varrast ja pani ühele neist 64 plaati puhast kulda, nii et iga väiksem ketas asetses suurema peal. Niipea kui kõik 64 ketast on nihutatud vardalt, mille peale Jumal Brahma need maailma loomise ajal asetas, teisele vardale, nihkuvad torn ja tempel tolmuks ning maailm sureb äikese all. Sõltumata Brahmast pakkus selle pusle välja 19. sajandi lõpul prantsuse matemaatik Eduard Luke. Müüdud versioonis kasutati tavaliselt 7-8 plaati (joonis 7). Joon. 7. Mõistatus "Hanoi torn". Oletame, et on olemas lahendus n-1 sõita. Siis vahetuseks n kettad, toimige järgmiselt: 1) Nihutame n-1 sõita. Alates juhtumist n \u003d 1, nihke algoritm on ilmne, siis induktsiooni abil, toiminguid (1) - (3) tehes, saame nihutada suvalise arvu kettaid. Looge rekursiivne protseduur, mis prindib kindla arvu ketaste jaoks kogu ülekandejada. Selline protseduur peaks igas oma kõnes printima teavet ühe nihke kohta (algoritmi punktist 2). Punktidest (1) ja (3) nihutamiseks nõuab protseduur ennast, vähendades ketaste arvu ühe võrra. // n - ketaste arv // a, b, c - pin-numbrid. Nihutamine toimub nööpnõelast a, // nööpnõelale b abinõelaga c. protseduur Hanoi (n, a, b, c: täisarv); alusta kui n\u003e 1, siis alusta Hanoit (n-1, a, c, b); writeln (a, "-\u003e", b); Hanoi (n-1, c, b, a); end else writeln (a, "-\u003e", b); lõpp; Pange tähele, et rekursiivselt kutsutud protseduuride komplekt moodustab sel juhul puu, mida liigutatakse vastupidises järjekorras. Parsimise ülesanne on arvutada avaldise väärtus olemasolevalt real, mis sisaldab aritmeetilist avaldist, ja sellesse kuuluvate muutujate teadaolevaid väärtusi. Aritmeetiliste avaldiste arvutamise protsessi saab esitada kahendpuuna. Tõepoolest, iga aritmeetiline operaator (+, -, *, /) nõuab kahte operandi, mis on ühtlasi aritmeetilised avaldised ja mida võib vastavalt pidada alamtredeks. Joon. 8 on toodud puu näide, mis vastab avaldisele: Joon. 8. Süntaksipuu, mis vastab aritmeetilisele avaldisele (6). Sellises puus on lõppsõlmed alati muutujad (siin x) või arvkonstandid ning kõik sisemised sõlmed sisaldavad aritmeetilisi operaatoreid. Operaatori käivitamiseks peate esmalt arvutama selle operandid. Seega tuleks joonisel toodud puu mööda lõppjärjestust mööda liikuda. Vastav sõlmede jada kutsus vastupidine Poola märge aritmeetiline avaldis. Süntaksipuu ehitamisel peaksite tähelepanu pöörama järgmisele funktsioonile. Kui on olemas näiteks avaldis ning liidame liitmise ja lahutamise toimingud vasakult paremale, sisaldab õige süntaksipuu plussi asemel miinus (joonis 9a). Sisuliselt vastab see puu avaldisele.Puu koostamist on võimalik hõlbustada, kui analüüsime avaldist (8), vastupidi, paremalt vasakule. Sel juhul puu viigiga. 9b, mis vastab puule 8a, kuid ei nõua märkide asendamist. Samamoodi peate paremalt vasakule analüüsima avaldisi, mis sisaldavad korrutamise ja jagamise operaatoreid. Joon. 9. Süntaksipuud väljenduseks a – b + c lugedes vasakult paremale (a) ja paremalt vasakule (b). See lähenemisviis ei välista rekursiooni täielikult. Kuid see võimaldab teil piirduda ainult ühe rekursiivse protseduuri üleskutsega, mis võib olla piisav, kui motiiv on hoolitseda maksimaalse jõudluse eest. Selle lähenemisviisi mõte on asendada rekursiivsed kõned lihtsa ahelaga, mis täidetakse nii palju kordi, kui rekursiivsete protseduuridega moodustatud puus on sõlme. Mida täpselt igal sammul tehakse, tuleks kindlaks teha sammu numbriga. Sammu numbri ja vajalike toimingute võrdlemine ei ole tühine ülesanne ja igal juhul tuleb see eraldi lahendada. Näiteks las k pesastatud silmused kasutaja poolt n sammud igas: I1 jaoks: \u003d 0 kuni n-1 tehke i2 jaoks: \u003d 0 kuni n-1 tehke i3 jaoks: \u003d 0 kuni n-1 tehke ... Kui k Kui olete eelnevalt teadmata, kirjutage need selgesõnaliselt, nagu ülalpool näidatud, on võimatu. Jaotises 6.5 näidatud tehnikat kasutades saate rekursiivse protseduuri abil vajaliku arvu pesastatud silmuseid: Protseduur NestedCycles (Indeksid: täisarvu massiiv; n, k, sügavus: täisarv); var i: täisarv; algab kui sügavus Rekursioonist vabanemiseks ja kõik ühe tsüklina taandamiseks arvestame, et kui nummerdada süsteemi numbrid süsteemis n, siis on igal etapil number, mis koosneb numbritest i1, i2, i3, ... või vastavatest väärtustest indeksimassiivist. St numbrid vastavad tsükliloendurite väärtustele. Etapi number tavalises kümnendarvuses: Sammute koguarv on n k. Olles sortinud nende numbrid komaarvude süsteemis ja teisendanud igaüks neist baasisüsteemiga n, saame indeksite väärtused: M: \u003d ümmargune (IntPower (n, k)); i jaoks: \u003d 0 kuni M-1 alustage arvuga: \u003d i; kui p: \u003d 0 kuni k-1, alustage indekseid: \u003d arv mod n; Arv: \u003d arvu div n; lõpp; DoSomething (indeksid); lõpp; Veelkord märgime, et meetod pole universaalne ja peate iga ülesande jaoks leiutama midagi erinevat. 1. Määratlege, mida rekursiivsed protseduurid ja funktsioonid teevad. (a) Mida prindib Rec (4) helistamisel allolev protseduur? Protseduur Rec (a: täisarv); algavad kirjutised (a); kui a\u003e 0, siis Rec (a-1); writeln (a); lõpp; (b) Milline on funktsiooni Nod väärtus (78, 26)? Funktsioon Nod (a, b: täisarv): täisarv; alusta, kui a\u003e b, siis Nod: \u003d Nod (a - b, b) muul juhul, kui b\u003e a, siis Nod: \u003d Nod (a, b - a) muidu Nod: \u003d a; lõpp; c) Mida trükitakse järgmiste protseduuridega, kui helistate A (1)? Protseduur A (n: täisarv); protseduur B (n: täisarv); protseduur A (n: täisarv); algavad kirjutised (n); B (n-1); lõpp; protseduur B (n: täisarv); algavad kirjutised (n); kui n (d) Mida prindib järgmine protseduur BT-le helistamisel (0, 1, 3)? Protseduur BT (x: reaalne; D, MaxD: täisarv); alusta, kui D \u003d MaxD, siis kirjuta (x), muidu alusta BT (x - 1, D + 1, MaxD); BT (x + 1, D + 1, MaxD); lõpp; lõpp; 2. Meieoboros - madu, mis võtab laiendatud kujul enda saba (joonis 14), on pikk Lläbimõõt ümber pea Dkõhu seina paksus d. Tehke kindlaks, kui palju saba ta suudab endasse kinni tõmmata ja mitu kihti saba pärast laotatakse? Joon. 14. Laiendatud meie boorod. 3. Puu jaoks joonisel fig. 10a näitavad sõlmede külastuste jada otsese, vastupidise ja lõpu indekseerimise järjekorras. 4. Esitage graafiliselt puu, mis on määratletud lisatud sulgudes: (A (B (C, D), E), F, G). 5. Joonistage järgmise aritmeetilise avalduse graafiline süntaksipuu: Kirjutage see väljend poola vastupidisesse märkusse. 6. Allpool oleva graafiku jaoks (joonis 15) kirjutage külgnevuse maatriks ja esinemissageduse maatriks. 1. Kui arvutate piisavalt palju kordi (miljon või enam) faktoriaal, võrrelge rekursiivsete ja iteratiivsete algoritmide tõhusust. Mitu korda teostusaeg erineb ja kuidas sõltub see suhe arvust, mille koefitsient arvutatakse? 2. Kirjutage rekursiivne funktsioon, mis kontrollib sulgude õiget paigutust stringi. Nõuetekohase paigutuse korral on täidetud järgmised tingimused: a) sulgude arv on võrdne. Näited valest paigutusest :) (, ()) (, ()) (() jne 3. Real võib olla sulgudes nii sulgudes kui ka nurksulgudes. Iga avaklamber vastab sama tüüpi sulgurile (ümmargune - ümmargune, ruudukujuline). Kirjutage rekursiivne funktsioon, mis kontrollib, kas sulud on sel juhul õiged. Vale paigutuse näide: ([)]. 4. Regulaarsete sulgudestruktuuride pikkusega 6 on 5: () () (), (()) (), () (()), ((())), (() ()). Märkus: Minimaalse pikkusega korrektuuri õige konstruktsioon “()”. Pikemad struktuurid saadakse lühematest struktuuridest kahel viisil: a) kui väiksem struktuur on toodud sulgudes, 5. Looge protseduur, mis prindib kõik võimalikud permutatsioonid täisarvudele 1 kuni N. 6. Looge protseduur, mis prindib kõik komplekti alamhulgad (1, 2, ..., N). 7. Koostage protseduur, mis prindib naturaalarvu N kõik võimalikud esindused teiste naturaalarvude summana. 8. Looge funktsioon, mis arvutab massiivi elementide summa vastavalt järgmisele algoritmile: massiiv jagatakse pooleks, arvutatakse mõlema poole elementide summad ja liidetakse need. Massiivi pooleks olevate elementide summa arvutatakse sama algoritmi järgi, see tähendab jällegi jagades pooleks. Jagunemised toimuvad seni, kuni massiivi moodustatud tükkides on üks element korraga ja summa arvutamine muutub vastavalt triviaalseks. Märkus: See algoritm on alternatiiv. Reaalselt hinnatud massiivide puhul võimaldab see tavaliselt saada väiksemate ümardamisvigade. 10. Koostage protseduur Kochi kõvera joonistamiseks (joonis 12). 11. Esitage pilt. 16. Joonisel on iga järgneva iteratsiooni korral ringid 2,5 korda väiksemad (selle koefitsiendi saab muuta parameetriks). 1. D. Knut. Programmeerimise kunst. t. 1. (punkt 2.3. "Puud"). Ettekande teemal "Rekursiivsed algoritmid" loodi selleks, et valmistada õpilasi ette arvutiteaduse ja IKT eksamiks. Töös käsitletakse rekursiooni määratlust, tuuakse näiteid rekursiivselt määratletud graafiliste objektide kohta. Ettekanne sisaldab meetodeid ülesande nr 11 lahendamiseks eksami demoversioonist - 2015 arvutiteaduse teemal. Esimene meetod hõlmab kõnepuu konstrueerimist, teine \u200b\u200bmeetod lahendab probleemi asendusmeetodi abil. Vaadeldakse 4 näidet ülesannete lahendamisest mõlema meetodi abil. Lisaks sisaldab esitlus 25 koolituse ülesannet koos vastustega Konstantin Poljakovi saidilt. Esitluste eelvaate kasutamiseks looge endale Google'i konto (konto) ja logige sisse: https://accounts.google.com Ülesande number 11 KASUTAMINE (põhitase, aeg - 5 minutit) Rekursiivsed algoritmid. Autor - Korotun OV, vastastikuse mõistmise memorandumi õpetaja "Keskkool number 71" Mida peate teadma: rekursioon - objekti või protsessi määratluses, kirjelduses, kujutises selle objekti või protsessi enda sees, see tähendab olukorda, kui objekt on osa iseendast. Vene Föderatsiooni vapp on rekursiivselt määratletud graafiline objekt: sellel kujutatud kahepäise kotka paremasse käppa on kinnitatud skeptik, mida kroonib vapi väike koopia. Kuna skept asub ka sellel embleemil kotka paremas käpas, saadakse lõpmatu rekursioon. Venemaa rekursiivne vapp Programmeerimisel on rekursioon kutsumine funktsioonile, mis pärineb sellest ise, otse või muude funktsioonide kaudu, näiteks funktsioon A kutsub funktsiooni B ja funktsioon B kutsub funktsiooni A. Funktsiooni või protseduuri pesastatud kõnede arvu nimetatakse rekursiooni sügavuseks. rekursiooni näide: kui kleitil on rasvane plekk, siis ärge muretsege. Õliplekid eemaldatakse bensiiniga.Õliplekid eemaldatakse leeliselahusega. Leelised eemaldatakse essentsiga. Pärast essentsi hõõruge õli ära. Noh, te juba teate, kuidas õliplekke eemaldada! Näidisülesanne: antud rekursiivne algoritm: protseduur F (n: täisarv); algavad kirjutised (n); kui n Näidisülesanne: antud rekursiivne algoritm: protseduur F (n: täisarv); algavad kirjutised (n); kui n Näidisülesanne: antud rekursiivne algoritm: protseduur F (n: täisarv); algavad kirjutised (n); kui n Slaid 9 Näidisülesanne: antud rekursiivne algoritm: protseduur F (n: täisarv); algavad kirjutised (n); kui n Slaid 10 Näidisülesanne: antud rekursiivne algoritm: protseduur F (n: täisarv); algavad kirjutised (n); kui n Slaid 11 15 Näide nr 2: Antud rekursiivne algoritm: protseduur F (n: täisarv); algavad kirjutised (n); kui n Näide nr 2: Antud rekursiivne algoritm: protseduur F (n: täisarv); algavad kirjutised (n); kui n Slide 13 Näide nr 3: Antakse rekursiivne algoritm: protseduur F (n: täisarv); algavad kirjutised ("*"); kui n\u003e 0, alustage F (n-2); F (n div 2) otsaotsa; Mitu tärnitähte trükitakse ekraanile, kui helistate numbrile F (7)? 7 5 3 2 3 1 1 1 1 Selles näites ei kuvata ekraanil parameetri n väärtust, vaid sümbolit * -2 div 2 1 0 -1 0 -1 0 -1 -1 -1 -1 0 0 0 Näide nr 3: Antakse rekursiivne algoritm: protseduur F (n: täisarv); algavad kirjutised ("*"); kui n\u003e 0, alustage F (n-2); F (n div 2) otsaotsa; Mitu tärnitähte trükitakse ekraanile, kui helistate numbrile F (7)? * Kui olete loendanud "tähtede" arvu, saame 21. Selles näites ei kuvata ekraanil parameetri n väärtusi, vaid sümbolit * * * * * * * * * * * * * * * * * * * * * * Näide nr 3: Antakse rekursiivne algoritm: protseduur F (n: täisarv); algavad kirjutised ("*"); kui n\u003e 0, alustage F (n-2); F (n div 2) otsaotsa; Mitu tärnitähte trükitakse ekraanile, kui helistate numbrile F (7)? Lahendame probleemi ilma puuta. Olgu S (n) tärnide arv, mis kuvatakse, kui helistate F (n). Siis 1 + S (n-2) + S (n div 2), n\u003e 0 1, n Peame välja selgitama S (7). S (7) \u003d 1 + S (5) + S (3) S (5) \u003d 1 + S (3) + S (2) S (3) \u003d 1 + S (1) + S (1) S ( 2) \u003d 1 + S (0) + S (1) \u003d 1 + 1 + S (1) \u003d 2 + S (1) S (1) \u003d 1+ S (-1) + S (0) \u003d 1 + 1 + 1 \u003d 3 Me teeme tagasikäigu: S (2) \u003d 2 + 3 \u003d 5 S (3) \u003d 1 + 3 + 3 \u003d 7 S (5) \u003d 1 + 7 + 5 \u003d 13 S (7) \u003d 1 + 13 + 7 \u003d 21 S (n) \u003d Näide nr 4: protseduur F (n: täisarv); algab, kui n Slaid 18 Näide nr 4: protseduur F (n: täisarv); algab, kui n Slaid 19 Näide nr 4: protseduur F (n: täisarv); algab kui n Näide nr 4: protseduur F (n: täisarv); algab kui n Treeningud 1. ülesanne: antud rekursiivne algoritm: protseduur F (n: täisarv); algavad kirjutised ("*"); kui n\u003e 0, alustage F (n-2); F (n div2); F (n div2); otsa lõpp; Mitu tärnitähte trükitakse ekraanile, kui helistate numbrile F (5)? Vastus: 34 2. ülesanne: antud rekursiivne algoritm: protseduur F (n: täisarv); algavad kirjutised ("*"); kui n\u003e 0, alustage F (n-2); F (n-2); F (n div2); otsa lõpp; Mitu tärnitähte trükitakse ekraanile, kui helistate numbrile F (6)? Vastus: 58 Ülesanne 3: antud rekursiivne algoritm: protseduur F (n: täisarv); algavad kirjutised ("*"); kui n\u003e 0, alustage F (n-3); F (n div2); otsa lõpp; Mitu tärnitähte trükitakse ekraanile, kui helistate numbrile F (7)? Vastus: 15 4. ülesanne: antud rekursiivne algoritm: protseduur F (n: täisarv); algavad kirjutised ("*"); kui n\u003e 0, alustage F (n-3); F (n-2); F (n div2); otsa lõpp; Mitu tärnitähte trükitakse ekraanile, kui helistate numbrile F (7)? Vastus: 55 5. ülesanne: antud rekursiivne algoritm: protseduur F (n: täisarv); algavad kirjutised ("*"); kui n\u003e 0, alustage F (n-3); F (n-2); F (n div2); F (n div2); otsa lõpp; Mitu tärnitähte trükitakse ekraanile, kui helistate numbrile F (6)? Vastus: 97 6. ülesanne: antud rekursiivne algoritm: protseduur F (n: täisarv); algavad kirjutised ("*"); kui n\u003e 0, alustage kirjutamist ("*"); F (n-2); F (n div2); otsa lõpp; Mitu tärnitähte trükitakse ekraanile, kui helistate numbrile F (7)? Vastus: 31 7. ülesanne: antud rekursiivne algoritm: protseduur F (n: täisarv); algavad kirjutised ("*"); kui n\u003e 0, alustage kirjutamist ("*"); F (n-2); F (n div2); F (n div2); otsa lõpp; Mitu tärnitähte trükitakse ekraanile, kui helistate numbrile F (7)? Vastus: 81 8. ülesanne: antud rekursiivne algoritm: protseduur F (n: täisarv); algavad kirjutised ("*"); kui n\u003e 0, alustage kirjutamist ("*"); F (n-2); F (n-2); F (n div2); otsa lõpp; Mitu tärnitähte trükitakse ekraanile, kui helistate numbrile F (6)? Vastus: 77 9. ülesanne: antud rekursiivne algoritm: protseduur F (n: täisarv); alusta, kui n\u003e 0, siis alusta F (n-2); F (n-1); F (n-1); lõpp; writeln ("*"); lõpp; Mitu tärnitähte trükitakse ekraanile, kui helistate numbrile F (5)? Vastus: 148 10. ülesanne: antud rekursiivne algoritm: protseduur F (n: täisarv); alusta, kui n\u003e 0, siis hakka kirjutama ("*"); F (n-2); F (n-1); F (n-1); lõpp; writeln ("*"); lõpp; Mitu tärnitähte trükitakse ekraanile, kui helistate numbrile F (5)? Vastus: 197 Ülesanne 11: Antakse rekursiivne algoritm: protseduur F (n: täisarv); alusta, kui n\u003e 1, siis alusta F (n-2); F (n-1); F (n div2); lõpp; writeln ("*"); lõpp; Mitu tärnitähte trükitakse ekraanile, kui helistate numbrile F (7)? Vastus: 88 Ülesanne 12: antud rekursiivne algoritm: protseduur F (n: täisarv); alusta, kui n\u003e 2, siis hakka kirjutama ("*"); F (n-2); F (n-1); F (n div2); lõpp; writeln ("*"); lõpp; Mitu tärnitähte trükitakse ekraanile, kui helistate numbrile F (6)? Vastus: 33 Ülesanne 13: Antud rekursiivne algoritm: protseduur F (n: täisarv); algavad kirjutised (n); kui n Ülesanne 14: Antakse rekursiivne algoritm: protseduur F (n: täisarv); algavad kirjutised (n); kui n Ülesanne 15: Antakse rekursiivne algoritm: protseduur F (n: täisarv); algavad kirjutised (n); kui n Ülesanne 16: antud rekursiivne algoritm: protseduur F (n: täisarv); algavad kirjutised (n); kui n Ülesanne 17: Antud rekursiivne algoritm: protseduur F (n: täisarv); algavad kirjutised (n); kui n 18. ülesanne: antud rekursiivne algoritm: protseduur F (n: täisarv); algavad kirjutised (n); kui n Ülesanne 19: Antakse rekursiivne algoritm: protseduur F (n: täisarv); algavad kirjutised (n); kui n Ülesanne 20: Antakse rekursiivne algoritm: protseduur F (n: täisarv); algavad kirjutised (n); kui n Ülesanne 21: antud rekursiivne algoritm: protseduur F (n: täisarv); algavad kirjutised (n); kui n Ülesanne 22: antud rekursiivne algoritm: protseduur F (n: täisarv); algavad kirjutised (n); kui n 23. ülesanne: antud rekursiivne algoritm: protseduur F (n: täisarv); algavad kirjutised (n); kui n 24. ülesanne: antud rekursiivne algoritm: protseduur F (n: täisarv); algavad kirjutised (n); kui n Ülesanne 25: Antakse rekursiivne algoritm: protseduur F (n: täisarv); algavad kirjutised (n); kui n
Tere, N 2
…
Tere, N 10
…
Tere, N 1
…
Tere, N 10
Tere, N 10
…
Tere, N 14. Korduvad suhted. Rekursioon ja kordamine
5. Puud
5.1. Põhimääratlused. Puude pildistamise viisid
a) Selle puu juureks on üks spetsiaalne sõlm.
b) Ülejäänud sõlmed (välja arvatud juur) sisalduvad paarisjoontes eraldatud alamhulkades, millest igaüks omakorda on puu. Puud on nn subtrees see puu.

5.2. Puude läbipääs
5.3. Puu kujutamine arvutimälus


6. Rekursiivsete algoritmide näited
6.1. Puu joonistamine

6.2. Hanoi tornid
Protsess nõuab, et suurem ketas ei oleks kunagi väiksema üle. Mungad on raskustes, mis järjekorras tasub nihutamist? Selle jada arvutamiseks on vaja varustada neid tarkvaraga.
2) nihutame nth ketas järelejäänud vaba pin.
3) nihutame virna alates n-1 lõikes 1 saadud ketas nth ketas.6.3. Aritmeetiliste avaldiste parsimine
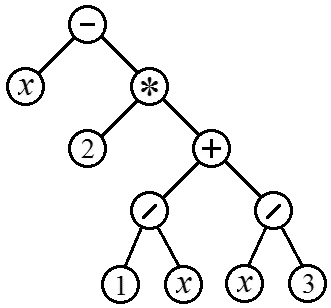

7.3. Puusõlme määramine selle arvu järgi
Turvaküsimused


Ülesanded
b) mis tahes avapaari sees - vastav sulg, sulud on õigesti paigutatud.
Kirjutage rekursiivne programm, et genereerida kõik tavalised sulgudestruktuurid pikkusega 2 n.
b) kui kaks väiksemat struktuuri on kirjutatud järjestikku.
Kirjandus
2. N. Wirth. Algoritmid ja andmestruktuurid.Laadige alla:
Eelvaade:
Slaidide pealkirjad:



